PF-ODE Sampling in Diffusion Models
Published:
📚 Table of Contents
- 1. Introduction
- 2. Numerical ODE Solver
- 3. Pseudo-Numerical Methods for Diffusion Models
- 4. High-Order and Semi-Analytic Solvers
- 4.1 DEIS
- 4.2 DPM-Solvers
- 4.2.1 Setup: from PF-ODE to a Exponentially Weighted Integral integral
- 4.2.2 $\varphi$-functions inside: From the integral to high-order updates
- 4.2.3 Single-step DPM-Solver
- 4.2.4 Parameterization, schedules, and guidance
- 4.2.5 Implementation notes (applies to orders 1/2/3)
- 4.2.6 Relation to DEIS and bridge to DPM-Solver++
- 4.3 DPM-Solver++
- 4.4 UniPC
- 5. References
Diffusion sampling via the Probability Flow Ordinary Differential Equation (PF-ODE) appears to be a standard ODE solving problem, but off-the-shelf ODE numerical methods rarely achieve the optimal balance between speed and quality. This article, based on core numerical analysis concepts (single-step vs. multi-step, explicit vs. implicit, as well as the roles of LTE and GTE), reviews traditional ODE numerical methods and explains why they are not suitable for diffusion model sampling. Then, the article explores, tailored to the semi-linear structural characteristics of PF-ODE, and introduces diffusion model-specific samplers, including pseudo-numerical samplers (PLMS, PNDM) and high-order/semi-analytical methods (DEIS, DPM-Solver/++, UniPC).
1. Introduction
Diffusion models involves a forward diffusion process that gradually adds Gaussian noise to data samples until they become pure noise, and a reverse process that learns to denoise this noise back to generate new samples.
Mathematically, the forward process can be modeled as a stochastic differential equation (SDE):
\[dx = f(x, t) \, dt + g(t) \, dw\]where $x$ is the state variable (e.g., an image), $t$ is the time step, $f(x, t)$ is the drift term, $g(t)$ is the diffusion coefficient, and $dw$ represents Wiener process. The reverse process, used for sampling, is another SDE that approximates the time-reversal of the forward SDE, incorporating a score function $\nabla_x \log p_t(x)$ (the gradient of the log-probability density), which is estimated by a neural network trained via score matching.
A crucial insight is that this reverse SDE has an equivalent deterministic representation through the probability flow ordinary differential equation (PF ODE):
\[\frac{dx}{dt} = f(x, t) - \frac{1}{2} g(t)^2 \nabla_x \log p_t(x)\]This equivalence stems from the fact that the PF ODE is derived to match the Fokker-Planck equation (which describes the evolution of probability densities) of the original SDE, ensuring that trajectories generated by solving the ODE backward (from $t = T$ at pure noise to $t = 0$ at clean data) produce the same marginal probability distributions as the stochastic SDE paths, but without injecting additional randomness. Thus, sampling reduces to numerically integrating this ODE, making the process deterministic and potentially more efficient, as it avoids the variance introduced by stochastic sampling while preserving the generative quality.
In this post, we first review the numerical methods for solving ODEs. Then, we analyze why we do not directly use ODE numerical solvers for sampling in diffusion models. Finally, we explore how to construct an efficient sampler based on the properties of PF-ODE for sampling.
2. Numerical ODE Solver
Numerical methods convert a continuous‐time initial-value problem into a sequence of discrete algebraic updates that march the solution forward in small time steps.
Numerical ODE solvers work by discretizing the continuous time domain into a sequence of time points: $t_0, t_1, …, t_{n-1}, t_n$, the interval between any two adjacent time steps is $h$, i,e,. $t_i=t_{i-1}+h$. Given an initial-value problem:
\[\frac{dx}{dt}=f(t,x),\ \ \ \ x(t_0)=x_0\]the Fundamental Theorem of Calculus rewrites the update over one step $h$:
\[x_{t_{i+1}}=x_{t_i}+\int_{t_i}^{t_{i+1}}f(t,x)dt\]Because the exact integrand $f(t,x)$ is unknown (it involves the unknown path $x$), numerical schemes replace that integral with a tractable quadrature formula built from sample slopes. The essential difference between different numerical methods lies in the different strategies they use to approximate this integral.
2.1 One-step vs Multi-step
This research dimension answers the question: “How much historical information is needed to computer $x_{t_{n+1}}$?”
2.1.1 One-step Methods
A one-step method uses only the information from the single previous point $(t_n, x_{t_n})$ to compute $x_{t_{n+1}}$, it does not care about earlier points like $x_{t_{n-1}}$, $x_{t_{n-2}}$, etc. That is to say, The information for $x_{t_{n+1}}$ is determined entirely by $x_{t_n}$ and some estimates of the slope within the interval $[t_n, t_{n+1}]$, we formalize as general form $x_{t_{n+1}}=\Phi(t_n, x_{t_n}, h)$
Some classic numerical one-step methods are listed as follows:
| Methods | Order | NFE | Sampling Points | Update (explicit form) |
|---|---|---|---|---|
| Euler | 1 | 1 | $t_n $ | \(x_{t_{n+1}} = x_{t_n} + h*f(t_n, x_{t_n})\) |
| Heun (RK2) | 2 | 2 | \(t_n \\ t_n+h\) | \(k_1=f(t_n, x_{t_n}) \\ k_2=f(t_n+{h}, x_{t_n}+{h}*k_1) \\ x_{t_{n+1}}=x_{t_n}+\frac{h}{2}*(k_1+k_2)\) |
| RK3 | 3 | 3 | \(t_n \\ t_n+\frac{h}{2} \\ t_n+h\) | \(k_1=f(t_n, x_{t_n}) \\ k_2=f(t_n+\frac{h}{2}, x_{t_n}+\frac{h}{2}k_1) \\ k_3=f(t_n+h, x_{t_n}-hk_1+2hk_2) \\ x_{t_{n+1}}=x_{t_n}+\frac{h}{6}(k_1+4k_2+k_3)\) |
| RK4 | 4 | 4 | \(t_n \\ (t_n+\frac{h}{2})(2\times) \\ t_n+h\) | \(k_1=f(t_n, x_{t_n}) \\ k_2=f(t_n+\frac{h}{2}, x_{t_n}+\frac{h}{2}k_1) \\ k_3=f(t_n+\frac{h}{2}, x_{t_n}+\frac{h}{2}k_2) \\ k_4=f(t_n+h, x_{t_n}+hk_3) \\ x_{t_{n+1}}=x_{t_n}+\frac{h}{6}(k_1+2k_2+2k_3+k_4)\) |
Geometrically, The integral on the right equals the signed area enclosed by the curve $f(t,x)$, the $t$-axis, and the vertical lines $t=t_i$ and $t=t_{i+1}$. Higher order numerical methods guarantee a better asymptotic error bound when all other factors (step size, stability, constants, arithmetic) are favourable.
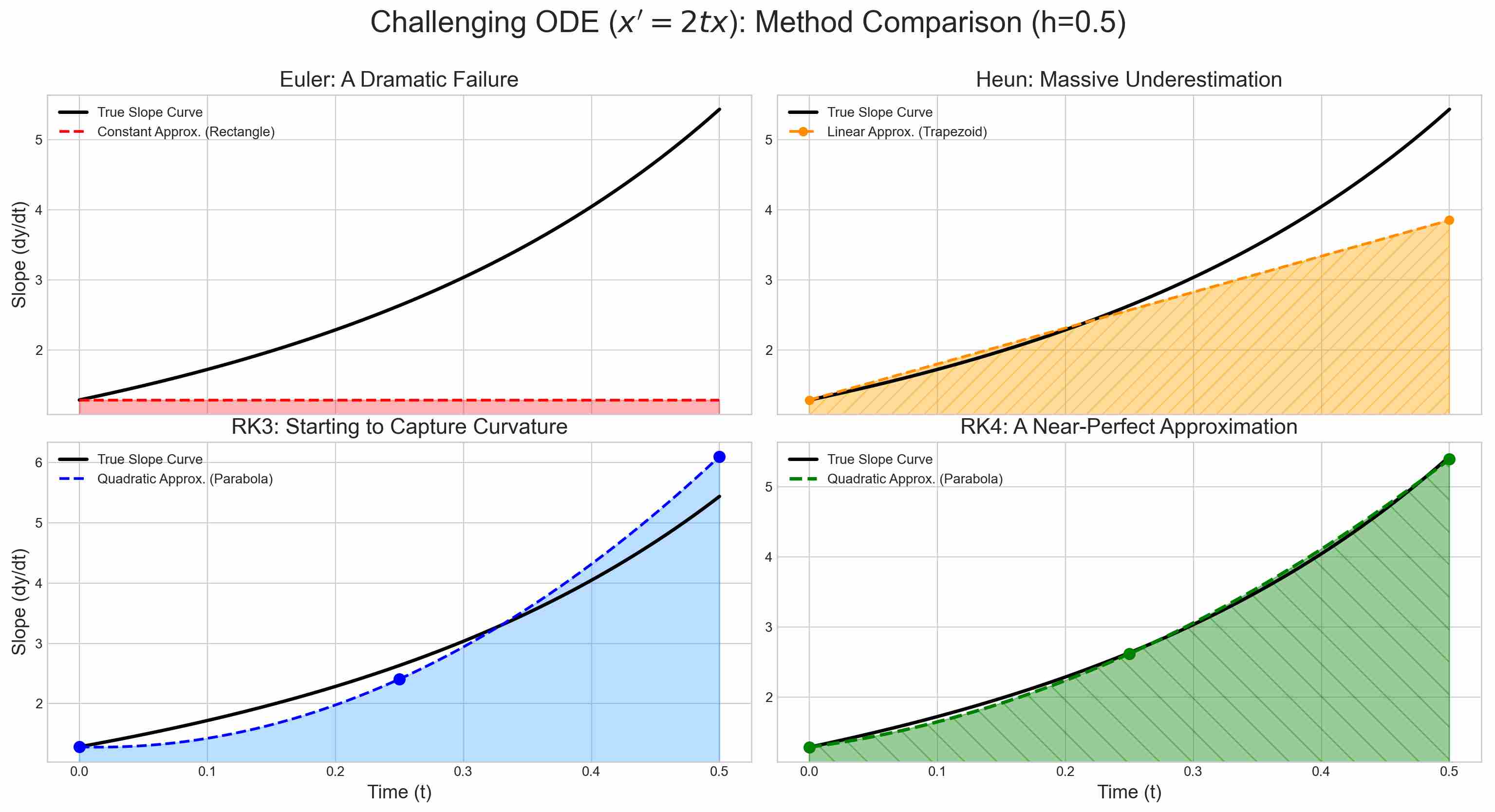
However, in real problems those factors often dominate, so a lower-order method can outperform a higher-order one.
2.1.2 Multi-step Methods
A multi-step method uses not only the information from the single previous point $(t_n, x_{t_n})$, but also from previous points, such as $(t_{n-1}, x_{t_{n-1}}), (t_{n-2}, x_{t_{n-2}})$, etc. We formalize this as a general form $x_{t_{n+1}}=\Phi(h, f_{n}, f_{n-1}, f_{n-2},\dots)$, where $f_i = f(t_i, x_{t_i})$. By leveraging historical slope evaluations ($f$ values from prior steps), these methods can achieve higher-order accuracy with fewer new function evaluations per step, making them more efficient for problems where $f$ is expensive to compute (like neural network calls in diffusion models). However, they require an initial “bootstrap” phase (often using one-step methods to generate the first few points) and can be less stable for non-smooth or stiff problems due to error propagation from history.
Traditional multi-step methods include the Adams family (Adams-Bashforth for explicit, Adams-Moulton for implicit) and Backward Differentiation Formulas (BDF) for stiff systems. Some classic numerical multi-step methods are listed as follows (focusing on explicit Adams-Bashforth variants for comparison with one-step methods; note that after bootstrapping, they typically require only 1 NFE per step as they reuse past $f$ values):
| Methods | Order | NFE | Sampling Points | Update (explicit form) |
|---|---|---|---|---|
| Adams-Bashforth 1 (AB1, equivalent to Euler) | 1 | 1 | $t_n$ | $x_{t_{n+1}}=x_{t_n}+hf(t_n,x_{t_n})$ |
| Adams-Bashforth 2 (AB2) | 2 | 1 | $t_n, t_{n-1}$ | $x_{t_{n+1}}=x_{t_n}+\frac{h}{2}[3f(t_n,x_{t_n})−f(t_{n−1},x_{t_{n−1}})]$ |
| Adams-Bashforth 3 (AB3) | 3 | 1 | $t_n, t_{n-1}, t_{n-2}$ | $x_{t_{n+1}}=x_{t_n}+\frac{h}{12}[23f(t_n,x_{t_n})−16f(t_{n−1},x_{t_{n−1}})+5f(t_{n−2},x_{t_{n−2}})]$ |
| Adams-Bashforth 4 (AB4) | 4 | 1 | $t_n, t_{n-1}, t_{n-2}, t_{n-3}$ | $x_{t_{n+1}}=x_{t_n}+\frac{h}{24}[55f(t_n,x_{t_n})−59f(t_{n−1},x_{t_{n−1}})+37f(t_{n−2},x_{t_{n−2}})−9f(t_{n−3},x_{t_{n−3}})]$ |
Geometrically, multi-step methods approximate the integral by fitting a polynomial interpolant through multiple past slope points, extrapolating forward. This can provide a more accurate area estimate under the curve $f(t,x)$ compared to one-step methods, especially for smooth functions, but it assumes the history is reliable—errors in early steps can compound over time.
The following figures Approximate $\int_{t_n}^{t_{n+1}}f(s, x(s))ds$ by integrating the Lagrange interpolant. The shaded region is the predicted area that advances the solution.
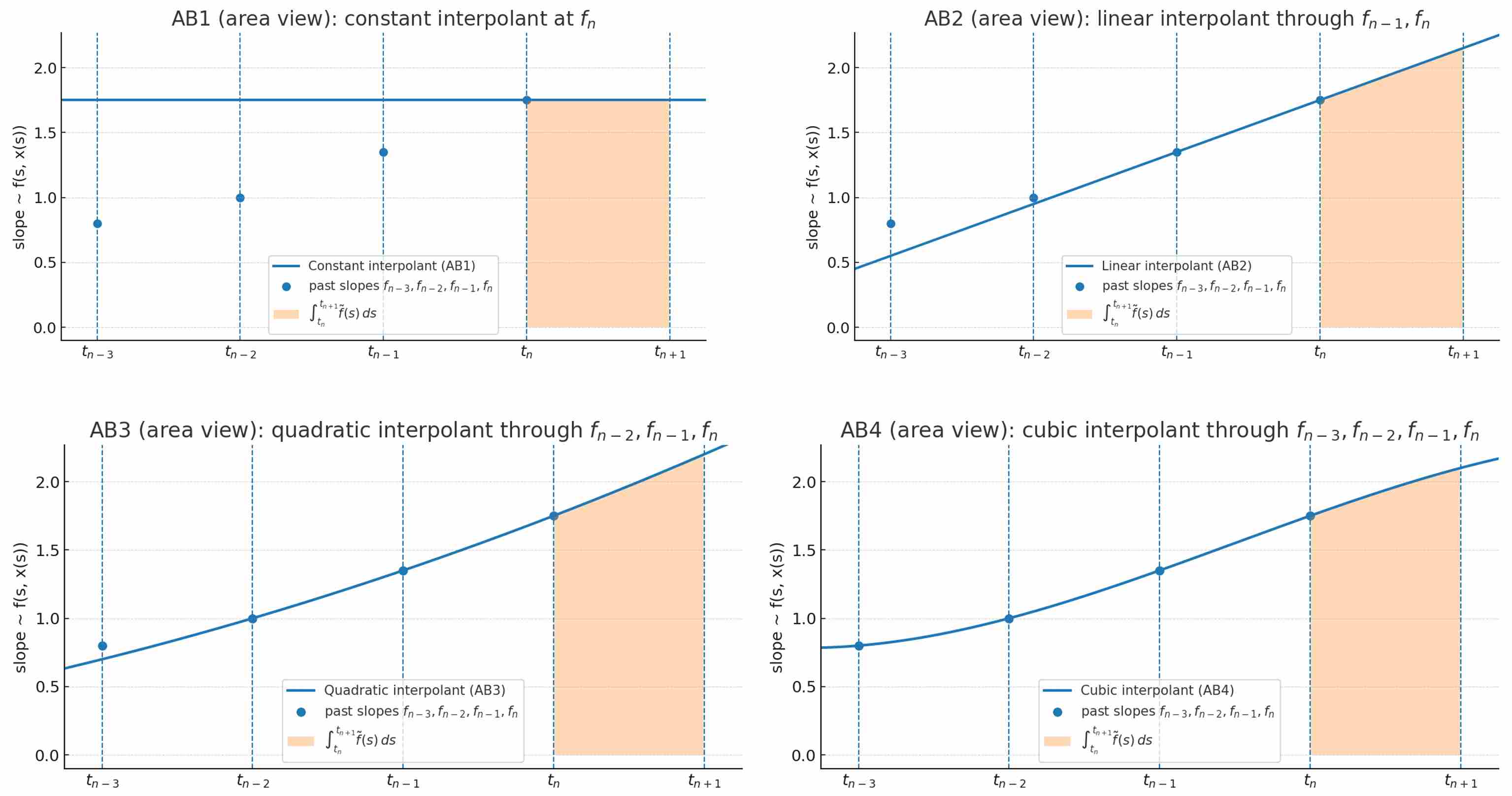
However, in practice, multi-step methods shine in scenarios with consistent step sizes and non-stiff ODEs, as they reduce computational overhead by recycling evaluations. For diffusion PF-ODEs, their efficiency inspires pseudo-multi-step samplers (e.g., PLMS), but stiffness often necessitates hybrid approaches with correctors or adaptive stepping.
2.2 Implicit vs Explicit
This research dimension aims to answer the question: “Is the formula for $x_{t_{n+1}}$ is a direct calculation or an equation to be solved?”, that is to say, whether $x_{t_{n+1}}$ appears on both sides of the equation simultaneously.
2.2.1 Explicit
Explicit methods refers to the formula for $x_{t_{n+1}}$ is an explicit expression, where the unknown $x_{t_{n+1}}$ appears only on the left-hand side. We can directly plug in known values on the right-hand side to compute $x_{t_{n+1}}$.
\[x_{t_{n+1}}=x_{t_n}+h\Phi(t_n, x_{t_n}, f_n, f_{n-1}, \dots)\]Where $f_n=f(t_n, x_{t_n})$. Examples include Forward Euler, explicit Runge–Kutta (Heun/RK3/RK4), and Adams–Bashforth (AB) multi-step schemes
2.2.2 Implicit
Implicit methods refers to the formula for $x_{t_{n+1}}$ is an equation, where the unknown $x_{t_{n+1}}$ appears on both sides of the equals sign. Typical examples including backward euler method, Adams-Moulton families.
\[x_{t_{n+1}}=x_{t_n}+h\Phi(t_{n+1}, x_{t_{n+1}}; t_n, x_{t_n}, f_n, f_{n-1}, \dots)\]An implicit method requires solving a (potentially nonlinear) equation at each step to find $x_{t_{n+1}}$, often using iterative techniques like Newton-Raphson. This increases computational cost per step but enhances stability, making them suitable for stiff ODEs common in diffusion models.
Some classic implicit numerical methods are listed as follows, focusing on Runge-Kutta family examples (which can be one-step; multi-step implicit methods like Adams-Moulton are also common):
| Methods | Order | NFE (per iteration) | Sampling Points | Update (implicit form) |
| Backward Euler | 1 | 1 (plus solver iterations) | $t_{n+1}$ | $x_{t_{n+1}} = x_{t_n} + h \cdot f(t_{n+1}, x_{t_{n+1}})$ |
| Trapezoidal (Implicit RK2) | 2 | 1 (plus solver iterations) | $t_n \ t_{n+1}$ | $x_{t_{n+1}} = x_{t_n} + \frac{h}{2} \left[ f(t_n, x_{t_n}) + f(t_{n+1}, x_{t_{n+1}}) \right]$ |
| Implicit Midpoint (Gauss-Legendre RK2) | 2 | 1 (plus solver iterations) | $t_n + \frac{h}{2}$ | $k = f\left(t_n + \frac{h}{2}, x_{t_n} + \frac{h}{2} k\right) \ x_{t_{n+1}} = x_{t_n} + h k$ |
| Radau IIA (Implicit RK3) | 3 | 2 (plus solver iterations) | $t_n + \frac{h}{3} \ t_n + h$ | Solve for $k_1, k_2$: \ $k_1 = f\left(t_n + \frac{h}{3}, x_{t_n} + \frac{5h}{12} k_1 - \frac{h}{12} k_2\right) \ k_2 = f\left(t_n + h, x_{t_n} + h k_1 + h k_2 - h k_1\right)$ (simplified Butcher tableau form; full details in literature) \ $x_{t_{n+1}} = x_{t_n} + \frac{3h}{4} k_1 + \frac{h}{4} k_2$ |
2.3 Local Truncation Error and Global Truncation Error
In numerical methods for solving ordinary differential equations (ODEs), errors arise because we approximate the continuous solution with discrete steps. Two key concepts are the Local Truncation Error (LTE) and the Global Truncation Error (GTE), which are the common indicators used to measure errors.
Local Truncation Error (LTE): This is the error introduced in a single step of the numerical method, assuming the solution at the previous step is exact. It measures how well the method approximates the true solution over one step, based on the Taylor series expansion of the exact solution.
Mathematically, if the exact solution at $t_n$ is $x(t_n)$, the LTE at step $n+1$ is:
\[\tau_{n+1} = x(t_{n+1}) - x_{n+1}^{\text{approx}}\]where $x_{n+1}^{\text{approx}}$ is computed using the method with exact input $x(t_n)$.
Global Truncation Error (GTE): This is the total accumulated error at the end of the integration interval (e.g., from $t_0$ to $T$), considering that errors from previous steps propagate forward. It depends on the number of steps $N = (T - t_0)/h$, and for stable methods, GTE is typically $O(h^p)$ if LTE is $O(h^{p+1})$. The relationship is roughly GTE $\approx$ (number of steps) $\times$ LTE, but propagation can amplify or dampen it.
Below, we will use the Euler method and the Henu method as examples to demonstrate how to obtain its LTE and GTE.
2.3.1 Example with Euler Method
The forward Euler method is a first-order method:
\[x_{n+1} = x_n + h f(t_n, x_n)\]Deriving LTE
Assume exact input: Start with $x_n = x(t_n)$.
The method approximates: $x_{n+1}^{\text{approx}} = x(t_n) + h f(t_n, x(t_n))$.
From Taylor: $x(t_n + h) = x(t_n) + hf(t_n, x(t_n)) + \frac{h^2}{2} x’‘(t_n) + O(h^3)$.
Subtract: LTE $\tau_{n+1} = x(t_n + h) - x_{n+1}^{\text{approx}} = \frac{h^2}{2} x’‘(t_n) + O(h^3)$.
Thus, LTE = $O(h^2)$. (The leading term is quadratic in $h$.)
This shows how to arrive: The Euler update matches the first two Taylor terms (constant + linear), so the error starts from the quadratic term.
Deriving GTE
Let $e_n = x(t_n) - x_n$ be the global error at step $n$.
The error recurrence: $e_{n+1} = e_n + h [f(t_n, x(t_n)) - f(t_n, x_n)] + \tau_{n+1}$.
For Lipschitz-continuous $f$ (with constant $L$), $|f(x(t_n)) - f(x_n)| \leq L |e_n|$, so: \(\|e_{n+1}\| \leq \|e_n\| (1 + h L) + \|\tau_{n+1}\|\)
Since $\tau_{n+1} = O(h^2)$, over $N$ steps ($N \approx 1/h$), the accumulated error bounds to $|e_N| \leq C h$ for some constant $C$ (from summing the geometric series of propagated local errors).
Thus, GTE = $O(h)$. (Errors accumulate linearly with $1/h$ steps, reducing the order by 1.)
Cause: Each local error adds up, and propagation (via $1 + hL$) amplifies like compound interest, but stability ensures it’s bounded by $O(h)$.
2.3.2 Example with Heun Method
The Heun method (a second-order Runge-Kutta) improves on Euler with a predictor-corrector:
\[k_1 = f(t_n, x_n), \quad k_2 = f(t_n + h, x_n + h k_1), \quad x_{n+1} = x_n + \frac{h}{2} (k_1 + k_2)\]Deriving LTE
Assume exact input: $x_n = x(t_n)$.
Expand $k_1 = f(t_n, x(t_n)) = x’(t_n)$.
Predictor: $x_n + h k_1 = x(t_n) + h x’(t_n)$.
$k_2 = f(t_n + h, x(t_n) + h x’(t_n))$. Taylor-expand $f$ in two variables:
\[\begin{align} f(t_n + h, x(t_n) + h x'(t_n)) = & f(t_n, x(t_n)) + h \left( f_t + x'(t_n) f_x \right) \\[10pt] & + \frac{h^2}{2} \left( f_{tt} + 2 x' f_{tx} + (x')^2 f_{xx} \right) + O(h^3) \end{align}\]But since $x’’ = \frac{\partial f}{\partial t} + x’ \frac{\partial f}{\partial x}$, $k_2 = x’ + h x’’ + \frac{h^2}{2} x’’’ + O(h^3)$.
Then, \(\begin{align} x_{n+1}^{\text{approx}} & = x(t_n) + \frac{h}{2} (x' + x' + h x'' + \frac{h^2}{2} x''' + O(h^3)) \\[10pt] & = x(t_n) + h x' + \frac{h^2}{2} x'' + \frac{h^3}{4} x''' + O(h^4) \end{align}\)
True: $x(t_n + h) = x(t_n) + h x’ + \frac{h^2}{2} x’’ + \frac{h^3}{6} x’’’ + O(h^4)$.
Subtract: LTE $\tau_{n+1} = \left( \frac{h^3}{6} - \frac{h^3}{4} \right) x’’’ + O(h^4) = -\frac{h^3}{12} x’’’ + O(h^4)$. Thus, LTE = $O(h^3)$. (Matches up to quadratic term, error from cubic.)
Deriving GTE
Similar recurrence:
\[\begin{align} e_{n+1} =\ & e_n + \frac{h}{2} [ (f(t_n, y(t_n)) - f(t_n, y_n))] \\[10pt] &+ \frac{h}{2}[(f(t_{n+1}, y(t_{n+1})) - f(t_{n+1}, y_n + h k_1)) ] + \tau_{n+1} \end{align}\]Using Lipschitz $L$, the perturbation terms are $O(e_n)$ and $O(h e_n + e_n)$, leading to $|e_{n+1}| \leq (1 + h L + O(h^2)) |e_n| + |\tau_{n+1}|$.
With $\tau_{n+1} = O(h^3)$, over $N \approx 1/h$ steps, the bound sums to $|e_N| \leq C h^2$ (accumulated as $N \times O(h^3) = O(h^2)$).
Thus, GTE = $O(h^2)$. (Higher local order leads to better global convergence.)
Cause: Fewer accumulations needed for the same accuracy, and the method’s stability (A-stable for some cases) prevents excessive propagation.
In summary, LTE is per-step (higher order means smaller), while GTE is overall (reduced by 1 order due to accumulation). For Euler (order 1), halving $h$ halves GTE; for Heun (order 2), it quarters GTE—making higher-order methods more efficient for accuracy.
2.4 The Limitation of Numerical ODE Solvers for diffusion Sampling
Although the PF ODE formulation enables deterministic sampling, directly applying standard numerical ODE solvers (e.g., explicit Runge-Kutta methods like RK4, Euler methods, or adaptive solvers like Dormand-Prince) is often suboptimal or problematic for diffusion models. These general-purpose solvers do not fully exploit the specific structure of diffusion ODEs, leading to inefficiencies and quality issues, particularly in high-dimensional spaces like image generation. Below, I list the key reasons, drawn from analyses of diffusion sampling challenges:
Numerical Instability and Stiffness Issues: Diffusion PF ODEs are semi-linear and can be stiff, especially in high dimensions, causing standard explicit solvers to become unstable with large step sizes. This results in exploding gradients or divergence, requiring tiny steps that increase computational cost and negate speed advantages.
High Discretization Errors in Few-Step Regimes: With fewer integration steps (e.g., 10–20 instead of 1000), traditional solvers accumulate significant truncation errors, causing the approximated trajectory to deviate from the true ODE path. This leads to degraded sample quality, such as artifacts or lower fidelity, as the solver fails to accurately track the probability flow.
Mismatch with Model Training Objectives: Diffusion models are trained to optimize score-matching losses, not to minimize ODE integration errors. Pursuing better ODE solving can paradoxically worsen perceptual quality, as seen in consistency models where tighter approximations to the PF ODE reduce sample fidelity due to inconsistencies between training and inference.
Inefficiency for Guided or Conditional Sampling: Standard solvers do not inherently handle constraints like classifier guidance or conditional generation efficiently, often requiring additional modifications that increase function evaluations (NFEs) or fail to maintain distribution matching.
Lack of Exploitation of Semi-Linear Structure: Diffusion ODEs have a specific semi-linear form (linear drift plus nonlinear score term), which general solvers ignore, leading to suboptimal performance. Without tailored approximations, they require more NFEs for convergence, making them slower than specialized methods.
These problems motivate the development of specialized solvers that incorporate higher-order approximations, exploit the ODE’s structure, and provide convergence guarantees for fast, high-quality sampling in low-NFE settings.
3. Pseudo-Numerical Methods for Diffusion Models
Now we apply the ODE numerical method to the diffusion model. PF-ODEs in diffusion have a semi-linear form
\[\frac{dx}{dt}=a(t)\,x + b(t)\,\underbrace{\mathcal{M}(x,t)}_{\epsilon_\theta,\ s_\theta,\ \text{or } v_\theta}.\]The linear drift $a(t)\,x$ is handled analytically via the training schedule (the $\alpha,\bar\alpha$ coefficients), so the step-to-step state update can be written as a closed one-step map (DDIM) that is linear in the model output for the current time. What we improve, then, is only the model output ($\mathcal{M}$) at the current step—using multistep extrapolation/correction—before plugging it into that one-step map.
Based on this observation, PNDM 1 use the same ideas of classical ODE methods (Section 2) but apply them to the model output only while the linear drift is absorbed by the schedule:
\[\frac{dx}{dt}=a(t)\,x + b(t)\,\underbrace{\mathcal{M}(x,t)}_{\epsilon_\theta,\ s_\theta,\ \text{or }v_\theta} \,\Rightarrow\, x_{t-\Delta}=\Psi\!\big(x_t,\ \widehat{\mathcal{M}}_t;\ \text{schedule}\big)\label{eq:17}\]- $\Psi$ is the schedule-aware one-step map (DDIM). It is linear in the model output and already handles the linear term $a(t)x$ analytically (integrating-factor view).
- The only thing we improve is $\widehat{\mathcal{M}}_t$ at the current step—via multistep extrapolation (PLMS) or in-step multi-stage blending (PRK).
Keypoint: treat the linear part exactly, raise the order on the neural part. This is the unifying principle behind the PNDM family.
3.1 PLMS - Pseudo Linear Multistep (Linear multi-step on model outputs)
PLMS 1 applies an Adams–Bashforth $k$-step formula to the model outputs, producing a more accurate $\widehat{\epsilon}_t$ (or $\widehat{s}_t,\widehat{v}_t$) before calling one step of $\Psi$. Take $\epsilon$-prediction as an example, PLMS improve the model output via multistep extrapolation like any ABK method
\[\hat\epsilon_{t} \;=\; \sum_{j=0}^{k-1} c^{(k)}_j\,\epsilon_{t-j} \quad\text{with}\quad \begin{cases} \text{AB2: } \ \hat\epsilon_t=\tfrac{3}{2}\epsilon_t - \tfrac{1}{2}\epsilon_{t-1}\\[2pt] \text{AB3: } \ \hat\epsilon_t=\tfrac{23}{12}\epsilon_t - \tfrac{16}{12}\epsilon_{t-1}+\tfrac{5}{12}\epsilon_{t-2}\\[2pt] \text{AB4: } \ \hat\epsilon_t=\tfrac{55}{24}\epsilon_t - \tfrac{59}{24}\epsilon_{t-1}+\tfrac{37}{24}\epsilon_{t-2}-\tfrac{9}{24}\epsilon_{t-3} \end{cases}\]After the model output is improved (from $\epsilon_{t}$ to $\hat\epsilon_{t}$), you then plug $\hat\epsilon_{t}$ into the one-step map $\Psi$ to get $x_{n-1}$. We apply the improved model output $\hat\epsilon_{t}$ to DDIM update
\[\hat x_0=\frac{x_t-\sqrt{1-\bar\alpha_t}\,\widehat{\epsilon}_t}{\sqrt{\bar\alpha_t}},\qquad x_{t-\Delta} =\sqrt{\bar\alpha_{t-\Delta}}\ \hat x_0+\sqrt{1-\bar\alpha_{t-\Delta}}\ \widehat{\epsilon}_t .\](For score or $v$ parameterizations, only the linear map between model output and $\hat x_0$ changes.)
like any k-step method, PLMS needs $k-1$ past outputs; initialize with DDIM or a short PRK. AB$k$ gives an $O(h^k)$ approximation to the IF-scaled slope (the model output after integrating-factor). Since $\Psi$ is linear in that output with bounded coefficients, the order transfers to the state (consistency + zero-stability).
After warm-up, PLMS uses one model evaluation per step (reuse history). It is fast and accurate in the 20–50 step regime; pure extrapolation can overshoot under very large steps or strong guidance—where a corrector or PRK warm-up helps.
3.2 PRK — Pseudo Runge–Kutta (in-step multi-stage on model outputs)
The core idea of PRK it to improve model output ($\widehat{\epsilon}_t,\,\widehat{s}_t,\,\widehat{v}_t$ using in-step stages (RK2/RK4) where intermediate states are obtained by $\Psi$ (DDIM update step, Equation \ref{eq:17}).
PRK2 (Heun-like) in equations
\[\begin{aligned} k_1 &= \epsilon_\theta(x_t,\ t),\\[8pt] x_{\text{mid}} &= \Psi\!\big(x_t,\ k_1;\ \tfrac{\Delta}{2}\big),\\[8pt] k_2 &= \epsilon_\theta\!\big(x_{\text{mid}},\ t-\tfrac{\Delta}{2}\big),\\[8pt] \widehat{\epsilon}_t &= \tfrac{1}{2}\,(k_1+k_2),\\[8pt] x_{t-\Delta} &= \Psi\!\big(x_t,\ \widehat{\epsilon}_t;\ \Delta\big). \end{aligned}\]PRK4 (RK4-like) in equations
\[\begin{aligned} k_1 &= \epsilon_\theta(x_t,\ t),\\[8pt] x^{(1)} &= \Psi\!\big(x_t,\ k_1;\ \tfrac{\Delta}{2}\big),\qquad k_2 = \epsilon_\theta\!\big(x^{(1)},\ t-\tfrac{\Delta}{2}\big),\\[8pt] x^{(2)} &= \Psi\!\big(x_t,\ k_2;\ \tfrac{\Delta}{2}\big),\qquad k_3 = \epsilon_\theta\!\big(x^{(2)},\ t-\tfrac{\Delta}{2}\big),\\[8pt] x^{(3)} &= \Psi\!\big(x_t,\ k_3;\ \Delta\big),\qquad k_4 = \epsilon_\theta\!\big(x^{(3)},\ t-\Delta\big),\\[8pt] \widehat{\epsilon}_t &= \tfrac{1}{6}\,\big(k_1+2k_2+2k_3+k_4\big),\\[8pt] x_{t-\Delta} &= \Psi\!\big(x_t,\ \widehat{\epsilon}_t;\ \Delta\big). \end{aligned}\]Compared with PLMS, PRK does not require warm-up. Instead, PRK is often used as a warm-up to seed PLMS history in the first few steps. The higher the order of the simulated RK, the higher the NFE of single-step for PRK.
3.3 Putting them together: the PNDM scheduler
A practical recipe that many implementations follow:
PRK warm-up (1–4 steps). Use RK2/RK4-style PRK to generate reliable early-step outputs and populate the history buffer.
PLMS main loop. Switch to PLMS (AB3/AB4 on model outputs) for speed: 1 NFE/step after warm-up.
(Optional) pseudo-corrector. If steps are very large or guidance is strong, add an AM-style blend on outputs (PECE): predict with AB → move with $\Psi$ → re-evaluate $\epsilon$ at the new end → correct with an AM-like average on outputs → final $\Psi$ move.
Implementation notes (applies to PLMS & PRK)
- Parameterization. The same designs work for $\epsilon$, score $s$, or $v$. Only the linear map inside $\Psi$ changes.
- Schedules. For non-uniform grids (Karras/EDM/ cosine), compute AB/AM weights from the current local grid; conceptually they are integrals of step-dependent Lagrange bases.
- Warm-up. If you skip PRK, a short DDIM or RK2 warm-up suffices to seed AB3/AB4.
- Guidance. Strong classifier-free guidance increases effective Lipschitz constants; prefer PRK warm-up and/or output-AM correction.
- Cost. PRK $>$ PLMS per step; PLMS wins on long runs. Both keep 1 linear $\Psi$ map per step; no implicit solve on the state is needed.
Takeaway. Pseudo-numerical samplers = high-order on model outputs + one schedule-aware state map. Read through section 2 with this in mind and you’ll see PLMS is the multistep (AB) track, PRK the multi-stage (RK) track, and the optional AM-style blend is the familiar predictor–corrector from classical ODEs—transplanted into diffusion with the integrating-factor lens.
4. High-Order and Semi-Analytic Solvers
The pseudo-numerical methods in section 3 (PNDM/PLMS/PRK) work impressively well in the mid-NFE regime, but they start to show structural limitations precisely when we push for very low NFE or strong classifier-free guidance. Their core idea—polynomial extrapolation of model outputs wrapped inside a one-step DDIM-style map—does not exploit the semi-linear nature of the probability-flow ODE. The linear drift is only approximated, so bias grows as steps get larger; stability regions are narrow, yielding oscillations or divergence under aggressive schedules and high guidance scales; multistep history creates warm-up fragility and makes step-grid changes brittle; and error constants tie tightly to the chosen time parameterization, so moving to non-uniform or log-SNR grids can be hit-or-miss. Most importantly, there is no principled route to raise order while preserving stability and schedule awareness—the coefficients are those of polynomial extrapolators, not of the underlying semi-linear flow. These shortcomings motivate section 4: a family of high-order, structure-exploiting ODE solvers (DEIS, DPM-Solver++, UniPC, etc.) that integrate the linear part exactly and apply higher-order, schedule-aware quadrature to the nonlinear/model part, delivering markedly better accuracy–stability trade-offs at 10–30 NFEs and under strong guidance.
4.1 DEIS
4.2 DPM-Solvers
DPM-Solver 2 is a family of high-order, structure-exploiting ODE solvers tailored to the probability-flow ODE (PF-ODE) of diffusion models. Instead of handing the entire right-hand side to a black-box ODE solver, it (i) solves the linear part analytically and (ii) changes variables from time $t$ to log-SNR space, which converts the nonlinear part into an exponentially weighted integral of the network output. Approximating that special integral with low-degree polynomials yields 1st/2nd/3rd-order updates that converge in the few-step regime.
4.2.1 Setup: from PF-ODE to a Exponentially Weighted Integral integral
Recall our discussion in previous post, the (backward) PF-ODE written with the forward process $(s,\sigma)$ pair and the model’s score $s_\theta$:
\[x_t=s(t)x_0+\sigma(t)\varepsilon\,\,\Longrightarrow\,\,\frac{dx_t}{dt}=f(t)x_t-\frac{g^2(t)}{2}s_{\theta}(x_t, t)\label{eq:20}\]with
\[f(t)=\frac{s'(t)}{s(t)}\quad \text{and} \quad g^2(t)=2\sigma(t)\sigma'(t)-2 \frac{s'(t)}{s(t)} \sigma^2(t)\]Using variation of constants over one step from $t_i$ to $t_{i-1}$ (backward integration), the exact one-step map decomposes into a linear part plus a nonlinear integral:
\[x_{t_{i-1}} = C_1 x_{t_i} + C_2\]where the linear coefficient is
\[C_1 = \exp\left( \displaystyle \int_{t_i}^{t_{i-1}} f(s) \, \mathrm{d}s \right) = \exp\left( \displaystyle \int_{t_i}^{t_{i-1}} \frac{s'(s)}{s(s)} \, \mathrm{d}s \right) = \frac{s(t_{i-1})}{s(t_i)}\label{eq:23}\]and the nonlinear term is
\[C_2 = - \exp\left( \displaystyle \int_{0}^{t_{i+1}} f(s) \, \mathrm{d}s \right) \displaystyle \int_{t_i}^{t_{i+1}} \frac{g^2(t)}{2} s_{\theta}(x_t, t) \exp\left( -\displaystyle \int_{0}^{t} f(s) \, \mathrm{d}s \right) \, \mathrm{d}t\]To further simplify this nonlinear term, we introduce log-SNR $\lambda(t)$:
\[\lambda(t) = \log \frac{s(t)}{\sigma(t)} \quad \Longrightarrow \quad \frac{\mathrm{d}\lambda(t)}{\mathrm{d}t} = \frac{\mathrm{d}\log s(t)}{\mathrm{d}t} - \frac{\mathrm{d}\log \sigma(t)}{\mathrm{d}t}\]A short calculation shows
\[\begin{align} g^2(t) & =2\sigma(t)\sigma'(t)-2 \frac{s'(t)}{s(t)} \sigma^2(t) \\[10pt] & = 2\sigma^2(t)\frac{\mathrm{d}\log \sigma(t)}{\mathrm{d}t} - 2\sigma^2(t)\frac{\mathrm{d}\log s(t)}{\mathrm{d}t} \\[10pt] & = -2\sigma^2(t)\frac{\mathrm{d}\lambda(t)}{\mathrm{d}t} \end{align}\]Changing variables $t \mapsto \lambda$ then collapses the nonlinear term into an exponentially weighted integral of $\epsilon_\theta$:
\[\begin{align} C_2 & = - \exp\left( \displaystyle \int_{0}^{t_{i-1}} f(s) \, \mathrm{d}s \right) \displaystyle \int_{t_i}^{t_{i-1}} \frac{g^2(t)}{2} s_{\theta}(x_t, t) \exp\left( -\displaystyle \int_{0}^{t} f(s) \, \mathrm{d}s \right) \, \mathrm{d}t \\[10pt] & = \int_{t_i}^{t_{i-1}} \sigma^2(t)\frac{\mathrm{d}\lambda(t)}{\mathrm{d}t} s_{\theta}(x_t, t) \exp\left( -\displaystyle \int_{t}^{t_{i-1}} f(s) \, \mathrm{d}s \right) \, \mathrm{d}t \\[10pt] & = \int_{t_i}^{t_{i-1}} \sigma^2(t)\frac{\mathrm{d}\lambda(t)}{\mathrm{d}t} \frac{-\epsilon_{\theta}(x_t, t)}{\sigma(t)} \exp\left( -\displaystyle \int_{t}^{t_{i-1}} f(s) \, \mathrm{d}s \right) \, \mathrm{d}t \\[10pt] & = -s(t_{i-1}) \int_{\lambda_{t_i}}^{\lambda_{t_{i-1}}} e^{-\lambda} \epsilon_{\theta}(x_{\lambda}, \lambda) \mathrm{d}\lambda\label{eq:32} \end{align}\]Putting equation \ref{eq:23} and equation \ref{eq:32} together, given an initial value $x_{t_i}$ at time $t=t_i$, the solution $x_{t_{i-1}}$ at time $t=t_{i-1}$ of diffusion ODEs in equation \ref{eq:20} is
\[\require{color} \definecolor{lightred}{rgb}{1, 0.9, 0.9} \fcolorbox{red}{lightred}{ $ \displaystyle x_{t_{i-1}} = \frac{s(t_{i-1})}{s(t_i)} x_t - s(t_{i-1}) \int_{\lambda_{t_i}}^{\lambda_{t_{i-1}}} e^{-\lambda} \, \epsilon_{\theta}(x_{\lambda}, \lambda) \, \mathrm{d}\lambda $ }\label{eq:33}\]To simplify notation, we denote $\epsilon_{\theta}(x_{\lambda}, \lambda)$ by $\epsilon_{\theta}(\lambda)$ (or simply $\epsilon_{\lambda}$) throughout this post. This identity is the starting point of DPM-Solver: the linear part is exact; all approximation effort is focused on the single exponentially weighted integral in $\lambda$.
Keypoint. PF-ODE has a semi-linear structure. Solving the linear drift exactly and approximating only the model-dependent part—under a log-SNR reparameterization—is what enables high order with very few NFEs.
4.2.2 $\varphi$-functions inside: From the integral to high-order updates
Define the log-SNR step size and a local coordinate on the interval:
\[h := \lambda_{t_{i-1}} - \lambda_{t_i} > 0, \qquad \tau := \lambda - \lambda_{t_i} \in [0,h]\]Then $ \lambda = \lambda_{t_i} + \tau$ and
\[e^{-\lambda} = e^{-(\lambda_{t_i}+\tau)} = e^{-\lambda_{t_{i-1}}}\,e^{\,h-\tau}\]Substitute into the integral in \ref{eq:33} and use $d\lambda=d\tau$:
\[\int_{\lambda_{t_i}}^{\lambda_{t_{i-1}}} e^{-\lambda}\,\epsilon_\theta(x_\lambda,\lambda)\,d\lambda = e^{-\lambda_{t_{i-1}}}\int_{0}^{h} e^{\,h-\tau}\, \epsilon_\theta\big(x_{\lambda_{t_i}+\tau},\lambda_{t_i}+\tau\big)\,d\tau.\]Since $s(t_{i-1})e^{-\lambda_{t_{i-1}}}=\sigma(t_{i-1})$, the nonlinear piece in \ref{eq:33} becomes
\[s(t_{i-1})\!\int e^{-\lambda}\epsilon_\theta\,d\lambda = \sigma(t_{i-1})\!\int_{0}^{h} e^{\,h-\tau}\, \epsilon_\theta\big(\lambda_{t_i}+\tau\big)\,d\tau\label{eq:37}\]Step 1 — Local Taylor model of the network output
Expand the noise-prediction $\epsilon_\theta$ in $\lambda$ around $\lambda_{t_i}$ (derivatives w.r.t. $\lambda$):
\[\epsilon_\theta(\lambda_{t_i}+\tau) = \sum_{m=0}^{p}\frac{\tau^m}{m!}\,\epsilon^{(m)}_i \;+\; \underbrace{\frac{\tau^{p+1}}{(p+1)!}\,\epsilon^{(p+1)}(\lambda_{t_i}+\xi_\tau)}_{\text{Lagrange remainder}}\label{eq:38}\]where $\epsilon_i := \epsilon_\theta(x_{t_i},\lambda_{t_i})$ and \(\epsilon^{(m)}_i := \partial_\lambda^m \epsilon_\theta(x_{\lambda},\lambda)\,\mid_{\lambda=\lambda_{t_i}}\)
Step 2 — Pull out the exponential weight and normalize the interval
Plug \ref{eq:38} into \ref{eq:37} and integrate term-by-term:
\[\int_0^h e^{\,h-\tau}\,\frac{\tau^m}{m!}\,d\tau = \frac{1}{m!}\, \underbrace{\int_0^h e^{\,h-\tau}\,\tau^m\,d\tau}_{\star}.\]Normalize $[0,h]$ to $[0,1]$ with $\theta=\tau/h$ (so $d\tau=h\,d\theta$):
\[\star \;=\; h^{m+1}\int_0^1 e^{\,h(1-\theta)}\,\theta^m\,d\theta\label{eq:40}\]Step 3 — Meet the $\varphi$-functions
The $\varphi$-functions 3 used in exponential integrators are defined by
\[\varphi_k(h) \;:=\; \int_0^1 e^{(1-\theta)h}\,\frac{\theta^{k-1}}{(k-1)!}\,d\theta \;\;=\;\; \sum_{r=0}^{\infty}\frac{h^r}{(r+k)!}, \quad k\ge 1,\]and satisfy the stable recurrences
\[\varphi_1(h)=\frac{e^h-1}{h},\quad \varphi_2(h)=\frac{\varphi_1(h)-1}{h},\quad \varphi_3(h)=\frac{\varphi_2(h)-\tfrac12}{h},\ \dots\]Comparing with (E) and setting $k=m+1$, we get the closed form
\[\int_0^h e^{\,h-\tau}\,\frac{\tau^m}{m!}\,d\tau = h^{m+1}\,\varphi_{m+1}(h)\label{eq:43}\]Step 4 — Assemble the unified series
Using \ref{eq:40} in \ref{eq:37} with \ref{eq:37}:
\[\int_{0}^{h} e^{\,h-\tau}\, \epsilon_\theta(\lambda_{t_i}+\tau)\,d\tau = \sum_{m=0}^{p} h^{m+1}\,\varphi_{m+1}(h)\,\epsilon^{(m)}_i \;+\; \underbrace{h^{p+2}\,\varphi_{p+2}(h)\,\widetilde{R}_{p+1}}_{\mathcal{O}(h^{p+2})},\]where \(\widetilde{R}_{p+1}\) collects a bounded combination of \(\epsilon^{(p+1)}\) on \([\lambda_{t_i},\lambda_{t_{i-1}}]\). Multiply by $\sigma(t_{i-1})$ and put everything back into \ref{eq:33}:
\[\require{color} \definecolor{lightred}{rgb}{1, 0.9, 0.9} \fcolorbox{red}{lightred}{ $ \displaystyle x_{t_{i-1}} = \frac{s(t_{i-1})}{s(t_i)}\,x_{t_i} \;-\; \sigma(t_{i-1})\Big[ h\,\varphi_1(h)\,\epsilon_i + h^2\,\varphi_2(h)\,\epsilon'_i + {h^3}\,\varphi_3(h)\,\epsilon''_i + \cdots \Big] $ }\]Approximating \(\epsilon'_i,\epsilon''_i,\dots\) with a small number of extra evaluations (finite differences in $\lambda$) yields practical 1/2/3-order schemes.
Takeaway. “Linear exact + $\varphi$-weighted polynomial” is the entire story. The $\varphi_k$ compress the exponential weight and the Taylor polynomial into stable, closed-form coefficients, enabling high order in few steps.
4.2.3 Single-step DPM-Solver (ε-prediction view)
Below we list the standard single-step (no history) formulas in the $\epsilon$-prediction parameterization. Using $x_0$- or $v$-prediction only changes the linear maps between the model head and $\epsilon$.
Order-1 (1-NFE). Constant approximation of $\epsilon$ over $[\lambda_i,\lambda_{i-1}]$:
\[x_{t_{i-1}} = \frac{s_{i-1}}{s_i}\,x_{t_i} \;-\; \sigma_{i-1}\,\varphi_1(h)\,\epsilon_i\]For small $h$ this matches a DDIM-like first-order step; for large $h$, $\varphi_1$ preserves the correct exponential scaling.
Order-2 (2-NFEs). One predict–correct to estimate $\epsilon’_i$.
- Predict with order-1 to get a provisional end state $\tilde x_{t_{i-1}}^{(1)}$.
- Evaluate $\epsilon_{i-1}^{(1)} := \epsilon_\theta(\tilde x_{t_{i-1}}^{(1)},\lambda_{t_{i-1}})$.
- Finite-difference $\epsilon’i \approx (\epsilon{i-1}^{(1)}-\epsilon_i)/h$ and plug into the mother formula:
Order-3 (3-NFEs). Two predictions to estimate \(\epsilon'_i,\epsilon''_i\).
- Predict to the midpoint $\lambda_{mid}=\lambda_i+\tfrac{h}{2}$ and to $\lambda_{i-1}$ (using order-1), yielding $\epsilon_{mid}^{(1)}$ and $\epsilon_{i-1}^{(1)}$.
Difference quotients:
\[\epsilon'_i \approx \frac{\epsilon_{mid}^{(1)}-\epsilon_i}{h/2}, \qquad \epsilon''_i \approx \frac{\epsilon_{i-1}^{(1)}-2\epsilon_{mid}^{(1)}+\epsilon_i}{(h/2)^2}.\]Update:
\[x_{t_{i-1}} = \frac{s_{i-1}}{s_i}\,x_{t_i}\;-\; \sigma_{i-1}\!\left[\varphi_1(h)\,\epsilon_i+ h\,\varphi_2(h)\,\epsilon'_i+ h^2\,\varphi_3(h)\,\epsilon''_i\right]\]
(Equivalently, use the “derivative-free” 3rd-order combination given in the original paper; it is algebraically identical to a second/third-order Hermite fit in $\lambda$.)
Heuristic. No guidance / small Lipschitz → order-3 often wins. Strong classifier-free guidance (CFG) / large steps → order-2 is typically more robust.
4.2.4 Parameterization, schedules, and guidance
- Parameterization ($\epsilon/x_0/v$). DPM-Solver works with any head; just map to $\epsilon$ before using the formulas, or carry a dual head and map back when needed. Data-prediction ($x_0$) variants are especially stable under strong guidance.
- Grids & schedules. The method is native to $\lambda$ (log-SNR) and plays well with non-uniform grids (e.g., Karras/EDM/cosine). Large $h$ is tempered by $\varphi_k(h)$ rather than pure polynomials.
- CFG. Guidance increases effective Lipschitz constants. Prefer order-2 single-step (or 1–2 order-2 warm-ups followed by order-3). Shrinking the first few $h$ values also helps.
4.2.5 Implementation notes (applies to orders 1/2/3)
Stable $\varphi_k$ evaluation. Use the recurrences
\[\varphi_1=\frac{e^h-1}{h},\quad \varphi_2=\frac{\varphi_1-1}{h},\quad \varphi_3=\frac{\varphi_2-\tfrac12}{h},\]plus series expansions when $|h|\ll 1$, to avoid cancellation.
- Time bookkeeping. Keep everything in $\lambda$ and store $(s_i,\sigma_i,\lambda_i)$ for each node.
- Clipping / thresholds. At extreme ends of the schedule (very small or very large $\lambda$), gentle clipping of $\lambda$ and/or $x_0$ (as in practice) can stabilize high-res runs.
- Cost model. Single-step order-2 needs 2 NFEs per step; order-3 needs 3. In the 10–30 NFE regime, the quality–stability trade-off is often superior to pseudo-numerical multistep methods.
4.2.6 Relation to DEIS and bridge to DPM-Solver++
- DEIS vs. DPM-Solver. Both exploit the semi-linear PF-ODE. DEIS uses an exponential-integrator discretization with polynomial extrapolation under an integrating factor; DPM-Solver absorbs the exponential weight into $\varphi_k$ coefficients in $\lambda$, yielding broader stability with closed-form weights in few steps.
- Toward DPM-Solver++. DPM-Solver++ systematizes these ideas under data-prediction, adds single-step and multistep variants, and introduces practical techniques (e.g., thresholding) for robust guided sampling. We will detail this in Section 4.3.
Takeaway. DPM-Solver converts PF-ODE’s structure—linear exactness + log-SNR exponential weight—into a concise algorithmic recipe: $\varphi$-functions times low-degree polynomials. This delivers high order at low NFE, and DPM-Solver++ carries the recipe into the strong-guidance regime.
4.3 DPM-Solver++
DPM-Solver++ 4 is a high-order solver designed specifically for guided sampling. It keeps the same structural exploit as section 4.2 (solve the linear part exactly; approximate the model term in $\lambda$-space) but switches to the data-prediction parameterization and couples it with thresholding and a multistep option to stabilize large guidance scales. In practice, this gives strong quality at 15–20 steps even with classifier(-free) guidance.
High-order noise-prediction solvers (including DPM-Solver, DEIS) can become unstable when the guidance scale grows, often losing to 1st-order DDIM at large scales. DPM-Solver++ addresses this by:
- Switching to data prediction (predict $x_0$ from $x_t$), which empirically enlarges the stability margin;
- Adding dynamic thresholding (clip the predicted $x_0$ into the data range);
- Providing multistep variants to shrink the effective step size.
Keypoint. DPM-Solver++ = “$\lambda$-space exponential integrator” + data-prediction $x_0$ + thresholding + optional multistep, targeted at the instability that high-order solvers exhibit under large guidance. ([arXiv][2])
4.3.1 Setup in $x_0$-prediction: exact one-step identity
We start from the standard PF-ODE
\[\frac{dx_t}{dt}=f(t)x_t-\frac{g^2(t)}{2}s_{\theta}(x_t, t)\]Switch to data prediction by expressing the score via the model’s $x_0$ head:
\[s_\theta(x_t,t)\;\approx\;-\frac{x_t-s(t)\,x_\theta(x_t,t)}{\sigma^2(t)}.\]Plugging this into the PF-ODE gives
\[\frac{dx_t}{dt} = \left(f(t) + \frac{g(t)^2}{2\sigma^2(t)}\right)\,x_t \;-\; \frac{g^2(t)}{2\sigma^2(t)}\,x_\theta(x_t, t).\]Under data prediction $x_\theta(x_\lambda,\lambda)\approx x_0$, the PF-ODE admits the exact log-SNR form (compare to $\epsilon$-view (section 4.2)):
\[\require{color} \definecolor{lightred}{rgb}{1, 0.9, 0.9} \fcolorbox{red}{lightred}{ $ \displaystyle x_{\lambda_t} = \frac{\sigma(t_{i-1})}{\sigma(t_i)}\,x_{t_i} \;+\;\sigma(t_{i-1})\,\int_{\lambda_{t_i}}^{\lambda_{t_{i-1}}} e^{\lambda}\,x_{\theta}(x_{\lambda},\lambda)\,d\lambda $ }\]This is the data-prediction counterpart of the $\epsilon$-view identity (which had $-\int e^{-\lambda}\epsilon_\theta\,d\lambda$). The linear coefficient scales by the $\sigma$ ratio, and the nonlinear term is now an $e^{\lambda}$-weighted integral of $x_\theta$.
Let $h=\lambda_{t_{i-1}}-\lambda_{t_i}>0$. Recenter the integral at the end of the step, $\theta=\lambda_{t_{i-1}}-\lambda\in[0,h]$:
\[\int_{\lambda_{t_i}}^{\lambda_{t_{i-1}}} e^{\lambda} x_\theta(\lambda)\,d\lambda = e^{\lambda_{t_{i-1}}}\!\int_{0}^{h} e^{-\theta}\,x_\theta(\lambda_{t_{i-1}}-\theta)\,d\theta.\]Taylor-expand $x_\theta(\cdot)$ in $\lambda$ about $\lambda_{t_i}$ or $\lambda_{t_{i-1}}$, and normalize $\theta=h\,u$. The resulting moments $\int_0^1 e^{-hu}u^m\,du$ can be written in terms of the $\varphi$-functions used in §4.2 via
\[\int_0^1 e^{-hu}\,\frac{u^{k-1}}{(k-1)!}\,du \;=\; e^{h}\,\varphi_k(h).\]Hence it is convenient to define $\hat\varphi_k(h):=e^{h}\varphi_k(h)$. With this, the unified mother formula for DPM-Solver++ becomes
\[\require{color} \definecolor{lightred}{rgb}{1, 0.9, 0.9} \fcolorbox{red}{lightred}{ $ \displaystyle x_{t_{i-1}} = \frac{\sigma(t_{i-1})}{\sigma(t_i)}\,x_{t_i} \;+\; s(t_{i-1})\Big[ \hat\varphi_1(h)\,x_{0,i} + h\,\hat\varphi_2(h)\,x'_{0,i} + \tfrac{h^2}{2}\,\hat\varphi_3(h)\,x''_{0,i} + \cdots\Big] $ }\] \[\boxed{ }\]where $x_{0,i}:=x_\theta(x_{t_i},\lambda_{t_i})$ and derivatives are w.r.t. $\lambda$. (Recall $e^{\lambda_{i-1}}=\frac{s_{i-1}}{\sigma_{i-1}}$.) This mirrors §4.2 but with a “plus” sign and the $\hat\varphi_k$ weights.
Takeaway. In ε-view (§4.2) the weight is $e^{-\lambda}$ and the linear factor is an $s$-ratio; in $x_0$-view (this section) the weight flips to $e^{+\lambda}$ and the linear factor is a $\sigma$-ratio. Both reduce to $\varphi$-weighted low-degree fits in $\lambda$.
4.3.2 Single-step DPM-Solver++ (data-prediction view)
Exactly as in §4.2, higher orders come from approximating $x’{0,i},x’‘{0,i}$ with a few extra evaluations.
Order-1 (1-NFE). Constant $x_0$ over $[\lambda_i,\lambda_{i-1}]$:
\[\boxed{ x_{t_{i-1}} = \frac{\sigma_{i-1}}{\sigma_i}\,x_{t_i} \;+\; \frac{s_{i-1}}{\sigma_{i-1}}\,\hat\varphi_1(h)\,x_{0,i} }\]This first-order limit is the DDIM step in $x_0$-prediction—DPM-Solver++ is its high-order generalization. ([arXiv][2])
Order-2 (2-NFEs). One predict–correct:
- Provisional end state via order-1;
- Evaluate $x_{0,i-1}^{(1)}:=x_\theta(\tilde x_{t_{i-1}}^{(1)},\lambda_{t_{i-1}})$;
- Use $\,x’{0,i}\approx(x{0,i-1}^{(1)}-x_{0,i})/h$ in the mother formula:
Order-3 (3-NFEs). Add a midpoint probe to estimate $x’{0,i},x’‘{0,i}$ (Hermite-style) and plug into the mother formula with $\hat\varphi_{2,3}$. As in §4.2, derivative-free closed forms exist (algebraically equivalent to using endpoint+midpoint combinations). ([arXiv][2])
Heuristic. With strong CFG, order-2 single-step is usually more robust; without guidance, order-3 can be slightly more accurate. (See also Diffusers’ doc recommendations.) ([Hugging Face][3])
4.3.3 Multistep DPM-Solver++ (2M)
The multistep variant reuses past evaluations of $x_\theta$ (data-prediction) to shrink the effective step size—similar spirit to Adams–Bashforth but derived in the same $\lambda$-space framework. In the guided regime this stabilizes high-order updates without extra NFEs per step after warm-up. The paper details both 2S (single-step) and 2M (multistep) instances and shows convergence in 15–20 steps on pixel-space and latent-space models. ([arXiv][2])
Keypoint. 2M reduces oscillations under large guidance by recycling history, while keeping the few-step speed advantage.
4.3.4 Thresholding (Imagen-style) and when to use it
Many image datasets have bounded dynamic ranges. Dynamic thresholding clips the predicted $x_0$ element-wise to a percentile-based bound before mapping back to $x_t$. In DPM-Solver++ this is straightforward because we are already in the $x_0$ view. It mitigates train–test mismatch and improves stability at high guidance scales. (Note: unsuitable for latent-space models like Stable Diffusion’s VAE latents; it’s for pixel-space models.) ([arXiv][2], [Hugging Face][4])
4.3.5 Practical recipe (what to actually use)
- Guided sampling (classifier or CFG): order = 2 (single-step or multistep).
- Unconditional sampling: order = 3 often gives a quality edge. These settings mirror common library defaults and tips (e.g., Diffusers). ([Hugging Face][3])
Takeaway. In practice, start with DPM-Solver++-2; enable 2M if steps are very few or guidance is large; use thresholding only for pixel-space models.
4.3.6 Relationship to §4.2 and to UniPC
- Versus §4.2 (ε-view). Same exponential-integrator skeleton, but the weight flips ($e^{-\lambda}\rightarrow e^{+\lambda}$) and the linear factor flips ($s$-ratio $\rightarrow$ $\sigma$-ratio). That (plus thresholding) explains the improved robustness under guidance.
- Bridge to §4.4 (UniPC). UniPC unifies/prunes coefficients from both single-step and multistep families (including ++), often offering a sweet spot in few-NFE regimes. We will pick up from this $x_0$-view to connect UniPC’s predictor–corrector forms.
4.4 UniPC
References
Liu L, Ren Y, Lin Z, et al. Pseudo numerical methods for diffusion models on manifolds[J]. arXiv preprint arXiv:2202.09778, 2022. ↩ ↩2
Lu C, Zhou Y, Bao F, et al. Dpm-solver: A fast ode solver for diffusion probabilistic model sampling in around 10 steps[J]. Advances in neural information processing systems, 2022, 35: 5775-5787. ↩
Hochbruck M, Ostermann A. Exponential integrators[J]. Acta Numerica, 2010, 19: 209-286. ↩
Lu C, Zhou Y, Bao F, et al. Dpm-solver++: Fast solver for guided sampling of diffusion probabilistic models[J]. Machine Intelligence Research, 2025: 1-22. ↩
